Q MATRIX

Computes the Q matrix for order 1 Tikhonov regularization

Contents

Function of MOBY-DIC TOOLBOX.

Description

This function computes the Q matrix for order 1 Tikhonov regularization. The Q matrix is used to regularize the Least Squares optimization

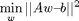
$$ \min_w || A w \textrm{--} b ||^2 $$

where w represents the array of the weights of the alpha basis in the definition of pwas function.

The regularized problems becomes

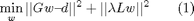
$$ \min_w || G w \textrm{--} d ||^2 + || \lambda L w ||^2 \qquad (1) $$

L is built in such a way to minimize the gradient of the pwas function defined by weights w. The structure of L is explained with this simple 2 dimensional example: consider this simplicial partition

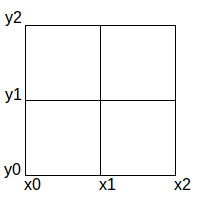
in which the weights are associated to the vertices as shown in the table below:

|   w1  |   w2  |   w3  |   w4  |   w5  |   w6  |   w7  |   w8  |   w9  |
|(x0,y0)|(x1,y0)|(x2,y0)|(x0,y1)|(x1,y1)|(x2,y1)|(x0,y2)|(x1,y2)|(x2,y2)|

The matrix L is such as the term 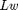$L w$ has this structure: 

(w2-w1)/(x1-x0)
(w4-w1)/(y1-y0)
(w3-w2)/(x2-x1)
(w5-w2)/(y1-y0)
(w6-w3)/(y1-y0)
(w5-w4)/(x1-x0)
(w7-w4)/(y2-y1)
(w6-w5)/(x2-x1)
(w8-w5)/(y2-y1)
(w8-w6)/(y2-y1)
(w8-w7)/(x1-x0)
(w9-w8)/(x2-x1)

which corresponds to the gradient of the pwas function computed in the vertices of the simplicial partition.

The Q matrix returned by this function is just the product 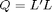$Q = L'L$.

Syntax

Q = QMatrix(D,P)

D is a matrix specifying the domain in the form: $$\left[ \begin{array}{cccc} x_{min}^1 & x_{min}^2 & \ldots & x_{min}^{nx}\\ x_{max}^1 & x_{max}^2 & \ldots & x_{max}^{nx} \end{array} \right] $$

P can be an array containing the number of subdivisions per dimensions (in case of uniform partition) or a cell array whose i-th element contains the i-th component of the vertices of the simplicial partition (for non-uniform partition).

Acknowledgements

Contributors:

Copyright is with:


Published with MATLAB® 7.8