HIERARCHICAL RIDGE REGRESSION
Performs a hierarchical PWAS constrained ridge regression on a set of data
Contents
Function of MOBY-DIC TOOLBOX.
Description
This function is very similar to function ridgeRegression. In function ridgeRegression a PWAS function is found which fits
data X and Y such that the error ![$[f(X)-Y]^2$](hierarchicalRidgeRegression_eq69936.png)
is minimal. In this function, many PWAS functions are computed such as their sum fits the data X and Y, in order to minimize:
![$$ \left[ \sum_{i=1}^{nfun} f_i(x) \textrm{--} Y \right]^2 $$](hierarchicalRidgeRegression_eq06066.png)
Each function %f_i% is a pwas function in the form:
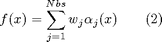
In this way the problem of the curse of dimensionality which affects the classical ridge regression solution, is softened. The weights to be computed are indeed less.
Syntax
[fpwas info] = hierarchicalRidgeRegression(X,Y,P)
X must be a cell array of matrices and Y a cell array of arrays. The number of cell arrays will coincide with the number of pwas function to be added. P defines the simplicial partition you want the fpwas functions to be defined on. If P is a scalar, each dimension of the domain of all pwas functions is subdivided into P intervals. If it is a cell array, you specify individually the number of subdivisions per dimension for each pwas function. Each element of cell array P can be an array or a cell array itself. The domain of the pwas function is automatically extrapolated from input data X and Xt. Xt and Yt (optional) represent a test dataset used to estimate the optimal value for the Tikhonov parameter lambda. lambda is chosen in order to minimize | f(Xt) - Yt |^2 being f the pwas function obtained starting from the training dataset (X,Y). If Xt and Yt are not provided, lambda is chosen with a GCV approach. Xt must be a [ndatatest x ndim] matrix and Yt a [ndatatest x 1] array.
fpwas is an array of pwas objects defining the pwas functions obtained after the regression which must be added to fit data Y.
info is a struct with the following fields:
- wnorm: it is the 2 norm of the weights vector w (for 0 order Tikhonov regularization) or the 2 norm of L w (for 1 order Tikhonov regularization)
- residual: it is the 2 norm of the residual G w - d ( i.e. f(X) - Y )
- test_error: it is the 2 norm of the residual computed in the test set (if provided), i.e. f(Xt) - Yt
[fpwas info] = hierarchicalRidgeRegression(X,Y,P,D)
As above, but the domain of the pwas functions is passed from outside the function. D is a cell array of matrices in the form:
![$$\left[ \begin{array}{cccc} x_{min}^1 & x_{min}^2 & \ldots & x_{min}^{nx}\\ x_{max}^1 & x_{max}^2 & \ldots & x_{max}^{nx} \end{array} \right] $$](hierarchicalRidgeRegression_eq17116.png)
Each element of the cell array is related to a pwas function.
[fpwas info] = hierarchicalRidgeRegression(X,Y,P,options)
options is a structure with the following fields:
- order: Tikhonov regularization order. It can be 0 or 1, default 0.
- lambda: regularization weight. It must be a scalar > 0. If it is not provided it is estimated inside the function.
- nsplits: number of splits of the dataset used to solve the regularised least square problem with an iterative
approach (in order to save memory). In practice, instead of solving
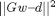, you can solve 
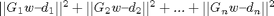, in which ![$G = [G_1 G_2 ... G_n]'$](hierarchicalRidgeRegression_eq40928.png)
and ![$d = [d_1 d_2 ... d_n]$](hierarchicalRidgeRegression_eq44096.png)
. nsplits corresponds to n. A low value of nsplits makes ridgeRegression faster but it can result
in memroy occupation problems. Default value, 1.
- gamma: domain expansion parameter. If the domain D is not provided from outside the function, it is automatically extrapolated from data X (and Xt). The tight domain (Dt) contains exactly data X. Such domain is increased of a factor gamma such as D = gamma Dt. Default value 1.1.
- solver: string specifying the solver you want to use to solve the QP problem (this is necessary only for constrained ridge regression, otherwise the solution is analytical). Possible choices are 'quadprog' (default), 'cvx', 'cplex', 'yalmip' 'clp'.
- verbose: if verbose is set to 1, messages are displayed indicating the status of the ridge regression process.
[fpwas info] = hierarchicalRidgeRegression(X,Y,P,D,options)
All fields explained above are specified.
Acknowledgements
Contributors:
- Tomaso Poggi (tpoggi@essbilbao.org)
Copyright is with:
- Copyright (C) 2010 University of Genoa, Italy.