CREATE CONSTRAINTS

Computes the matrices defining equality and inequality constraints for the pwas approximation of a control function.

Contents

Function of MOBY-DIC TOOLBOX.

Description

MPC control is generally required to satisfy constraints on system inputs and states. When a pwas approximation of a MPC control function is performed, such constraints must be enforced also on the approximated function. To do this the constraints must be enforced on the weights of the basis function expansion of the pwas object. This function, given state and input constraints as a constraints object, computes matrices A and B which impose the same constraints on the weights of the pwas function, with a dipendence of a possible slack variable sigma, in the form:

$$ A [w \sigma]' <= B \qquad (1) $$

The procedure to perform this operation is described below.

For constraints involving only inputs, in the form:

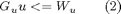
$$ G_u u <= W_u \qquad (2) $$

u is written as weighted sum of basis functions:

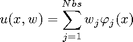
$$ u(x,w) = \sum_{j=1}^{Nbs} w_j \varphi_j(x) $$

or in vector form:

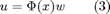
$$ u = \Phi(x) w \qquad (3) $$

Since u is pwas it is sufficient to impose these constraints only on the vertices of the simplicial partition, to guarentee that they are satisfied everywhere. By substituting (3) computed in the vertices of the simplicial partition in (2), it is easy to obtain:

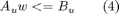
$$ A_u w <= B_u \qquad (4) $$

State constraints or mixed input-state constraints in the form:

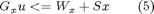
$$ G_x u <= W_x + S x \qquad (5) $$

are evaluated, as for constraints (2) in the vertices of the simplicial partition (only in the ones inside the feasibility domain of the pwag function). Since these constraints could not be imposed everywhere (also in the MPC formulation they can be softened), a slack variable is introduced to soften them. By substituting (3) computed on all vertices in (5), and by adding a slack variable it is easy to write (5) as:

$$ A_x [w \sigma]' <= B_x \qquad (6) $$

For state constraints or mixed input-state constraints in the form:

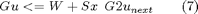
$$ G u <= W + S x - G2 u_{next} \qquad (7) $$

u is the control function at the current instant (the only one we want to approximate) and u_next contains all the optimal predicted control moves at subsequent time instants. These constraints must be enforced on the vertices of the simplicial partition, of the irregular partition and of the mixed partition which are contained in the feasibility domain of the control function. Due to a different structure of the partition between pwag and pwas functions, these constraints must be softened by means of a slack variable sigma (see also function L2Approx). By substituting (3) computed on all vertices in (7), and by adding a slack variable it is easy to write (7) as:

$$ A_p [w \ \sigma]' <= B_p \qquad (8) $$

By combining (4) with (6) and (8) it is possible to obtain constraints (1).

Matrices Aeq and Beq enforcing equality constraints in the form

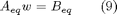
$$ A_{eq} w = B_{eq} \qquad (9) $$

can also be computed, if requested. These constraints can enforce either that pwas function is equal to optimal function in a region around the reference state, or that pwas function is zero in the reference state. These constraints can help achieving stability for regulation problems.

Syntax

[A,B,Aeq,Beq,d_w,d_sigma,VsTot,V,uV] = createConstraints(Upwas,U, linSys, constr, options)

Upwas is a pwas object defining just the pwas function space (i.e. domain, partion) and type of basis function.

U is a pwag object defining the optimal control function.

linSys is a linearSystem object defining the system which is controlled by pwag controller U.

constr is a constraints object defining the constraints you want the pwas approximated controller to satisfy.

options is a structure with following fields:

A and B are the matrices defining the inequality constraints (1).

Aeq and Beq are the matrices defining the equality constraints (9).

d_w is the number of weights w.

d_sigma is the number of slack variables.

VsTot is a matrix whose rows are all the vertices of the simplicial partition.

V is a matrix whose rows are the vertices of the simplicial, irregular and mixed partition inside the feasibility domain.

uV contains the value of the pwag function in vertices V.

Acknowledgements

Contributors:

Copyright is with:


Published with MATLAB® 7.8