COMPUTE MATRICES

Computes the matrices defining the quadratic cost function for the pwas approximation of a control function

Contents

Function of MOBY-DIC TOOLBOX.

Description

The pwas approximation of a control function with L2 norm or Least Squares approach is obtained by minimizing the following cost function:

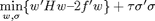
This function returns the matrices H and f. For L2 norm the ij-th element of matrix H is the integral on the feasibility domain of the product between the i-th and j-th basis function and the i-th element of vector f is the integral on the feasibility domain of the product between the optimal control function and the i-th basis function. For Least Squares approximation the ij-th element of matrix H is the sum of the products between the i-th and j-th basis function computed on some points in the feasibility domain and the i-th element of vector f is the sum of the products between the optimal control function and the i-th basis function computed on some points in the feasibility domain.

Syntax

[H, f] = computeMatrices(Upwas,U,L2)

U is the pwag object defining the optimal control function to approximate. Upwas is the pwas object defining the structure (domain and partition) of the approximated control function. L2 is a flag, if it is 1 the matrices H and f are the ones used for L2 norm approximation (see L2Approx); if it is 0, the matrices are related to Least Squares approximation (see LeastSquaresApprox). In case L2 = 1, the elements of the matrices (integrals) are computed with Euler approximation by sampling each of the hyper-rectangles composing the simplicial partition with 5^dim points on a regular grid. In case L2 = 0, the elements of matrices H and f are computed by summing on points created on a regular grid (using 5 Nx points per dimension, being Nx the number of partitions per dimension).

[H, f] = computeMatrices(Upwas,U,L2,nsamples)

If L2 = 0, nsamples is the number of points for dimensions which are used to sample the domain. If nsamples is a scalar value, the same number of points is used on all dimensions. If L2 = 1, nsamples is the number of points for dimensions which are used to sample each hyper-rectangle composing the simplicial partition. If nsamples is a scalar value, the same number of points is used on all dimensions.

[H, f] = computeMatrices(Upwas,U,L2,X)

Can be used if L2 = 0; X are the points used to sample the domain.

[H, f] = computeMatrices(Upwas,U,L2,X,Y)

Can be used if L2 = 0; X are the points used to sample the domain and Y the values of the optimal function on those points.

Acknowledgements

Contributors:

Copyright is with:

Published with MATLAB® 7.8