LINF APPROX

Performs a constrained PWAS approximation of a pwag control function with L infinity norm minimization

Description
Syntax
Acknowledgements

Description

Given a linearSystem object, a constraints object and a control function represented as a pwag object, this function returns a pwas object which approximates the pwag control function and satisfies (at its best) the constraints. The approximation is obtained by minimizing the L infinity norm of the difference between the optimal function U and the approximated one Upwas:

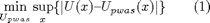
$\min_{U_{pwas}} \sup_x \{ |U(x) \textrm{--} U_{pwas}(x) | \} \qquad (1)$

Due to the piecewise affine linearity of the difference of the functions, the sup is obviously located in one of the vertices v of the simplicial, irregular or mixed partition. So (1) can be recast as:

$\min_{U_{pwas}} \max_v \{ |U(v) \textrm{--} U_{pwas}(v) | \}$

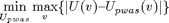
Any pwas function can be expressed as a weighted sum of basis functions in the form:

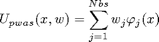
$U_{pwas}(x,w) = \sum_{j=1}^{Nbs} w_j \varphi_j(x)$

where 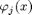$\varphi_j(x)$ can be the alpha, beta or psi basis and Nbs is the number of vertices of the simplicial partition. The above functional (1) can be recast as a function of weights w in this way:

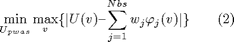
$\min_{U_{pwas}} \max_v \{ |U(v) \textrm{--} \sum_{j=1}^{Nbs} w_j \varphi_j(v) | \} \qquad (2)$

The minimization of this function can be performed with an LP problem in this way:

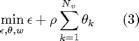
$\min_{\epsilon,\theta,w} \epsilon + \rho \sum_{k=1}^{N_v} \theta_k \qquad (3)$

subject to:

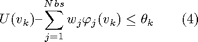
$U(v_k) \textrm{--} \sum_{j=1}^{Nbs} w_j \varphi_j(v_k) \leq \theta_k \qquad (4)$

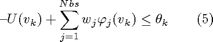
$\textrm{--} U(v_k) + \sum_{j=1}^{Nbs} w_j \varphi_j(v_k) \leq \theta_k \qquad (5)$

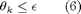
$\theta_k \leq \epsilon \qquad (6)$

for k = 1, ..., Nv, being Nv the number of vertices of the simplicial, irregular and mixed partition.

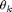$\rho$ is a coefficient weighting the terms $\theta_k$ . If rho = 0 the approximating function will minimize the infinity norm but can be very dissimilar from the original function. If rho is to high the infinity norm could not be minimized.

The pwas approximated function is moreover requested to satisfy the constraints specified in constraints object. Such constraints involve system inputs, states or both. Moreover they could be applied not only for the current time instant but also for the following, within a given prediction horizon. All these constraints can be recast as constraints involving only Upwas, in the form

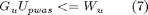
$G_u U_{pwas} <= W_u \qquad (7)$

or as constraints involving Upwas and the state x:

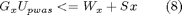
$G_x U_{pwas} <= W_x + S x \qquad (8)$

or as constraints involving Upwas, the state x and the optimal control function in future time instants (as provided by MPC technique):

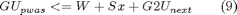
$G U_{pwas} <= W + S x + G2 U_{next} \qquad (9)$

Constraints (7) and (8) are imposed on all vertices of the simplicial partition, while constraints (9) are imposed on all vertices of simplicial, irregular and mixed partition lying inside the feasibility domain. The vertices of the irregular partition are the vertices of the partition of the pwag object, the vertices of the mixed partition are the vertices of the partition obtained by intersecting the simplicial with the irregular partitions. The feasibility domain is the domain in which the pwag function is defined. Constraints (8) and (9) could not be satisfied at all, due to constraints (7) and to the different partition structure. For these reason they are softened with a slack variable sigma, whose value is minimized in the optimization problem (3), which becomes

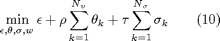
$\min_{\epsilon,\theta,\sigma,w} \epsilon+\rho \sum_{k=1}^{N_v} \theta_k + \tau \sum_{k=1}^{N_{\sigma}} \sigma_k \qquad (10)$

subject to (4), (5), (6) and

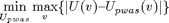
$\sigma_k >= 0 \qquad (11)$

for k = 1, ..., 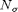$N_{\sigma}$ .

You can choose if use a slack variable for each vertex or a unique slack variable. Constraints (7), (8) and (9) can be written in dependence of weights w and slack variable sigma in this form:

$A [w \ \sigma]' <= B \qquad (12)$

Some other equality constraints can be enforced, if requested, of type:

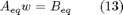
$A_{eq} w = B_{eq} \qquad (13)$

These constraints can enforce either that Upwas is equal to U in a region around the origin, or that Upwas is zero in the origin. These constraints can help achieving stability for regulation to origin problems.

At the end, this function finds a pwas function approximating the optimal one by solving (10) subject to (7), (8), (9), (11), (12) and (13).

Syntax

[Upwas sigma] = LInfApprox(Upwas, U, linSys, constr, options)

Input Upwas is a pwas object defining just the pwas function space (i.e. domain, partion) and type of basis function.

U is a pwag object defining the optimal control function.

linSys is a linearSystem object defining the system which is controlled by pwag controller U.

constr is a constraints object defining the constraints you want the pwas approximated controller to satisfy.

options is a structure with following fields:

solver: indicates the solver to be used for the optimization problem. Available solvers are 'linprog', 'cvx', 'cplex', 'clp', 'cdd', 'glpk'.

tau: weight for the slack variable sigma. The slack variables are necessary because some of the constraints (tipically the state constraints) could not be satisfied by the pwas approximated function, due to the different partition structure. If tau < 0 only one slack variable is used to soften all constraints else a variable for each vertex is used.

rho: weight for variables theta_k. If rho = 0, the optimization problem is easier, the infinity norm is minimized but the shape of the function can be very dissimilar to the original one. If rho is too high, the infinity norm could not be minimized.

equality: if equality is set to 1, local optimality constraints (8) are considered. If it is set to 2, the approximated control is constrained to be 0 in the origin.

verbose: if verbose is set to 1, messages are displayed indicating the status of the approximation process.

xref: reference state. The MPC control function is designed to bring the system state to xref

Output Upwas is the approximated pwas function object.

sigma is another pwas object defining the slack variable sigma.

Acknowledgements

Contributors:

Alberto Oliveri (alberto.oliveri@unige.it)
Tomaso Poggi (tpoggi@essbilbao.org)

LINF APPROX

Contents

Description

Syntax

Acknowledgements