IDENTIFY

Identifies the virtual sensor starting from the measured system inputs and outputs

Description
Syntax
Acknowledgements

Description

This function identifies a pwas virtual sensor starting from measures of system inputs (u), system measurable outputs (y) and system outputs (z) measurable only for a finite time window. It can be used for pwas discrete time system identification too. The observer is identified starting from T samples of input u, of the measurable output y and of the unmeasurable output z of the observed system. The weigths of the pwas map are estimated with a Regularized Least Square regression (see function ridgeRegression).

Syntax

object = identify(object,u,y,z,P,[ut],[yt],[zt])

u is a [npoints x nu] matrix whose i-th row corresponds to the i-th measurement of the nu inputs of the system. The same is for y (for the measurable outputs) and z (for the unmeasurable outputs). u, y and z can also be cell arrays whose i-th element correspond to a dataset obtained iterating the system starting from different initial conditions. P is an array containing the number of subdivisions per dimension of the simplicial partition. The domain of the pwas function is estimated from data. ut, yt and zt (optional) are matrices or cell arrays just as u, y and z, but they contain a test dataset which can be used to estimate the best value of the regularization parameter lambda. If they are not provided the optimal value for lambda is computed with a Generalized Cross Validation technique.

object = identify(object,u,y,z,P,[ut],[yt],[zt],D)

The domain is provided from outside the function. D is a matrix in the form: $\left[ \begin{array}{cccc} x_{min}^1 & x_{min}^2 & \ldots & x_{min}^{nx}\\ x_{max}^1 & x_{max}^2 & \ldots & x_{max}^{nx} \end{array} \right]$

object = identify(object,u,y,z,P,[ut],[yt],[zt],D,options)

options is a structure with the following fields:

order: Tikhonov regularization order. It can be 0 or 1, default 0.
lambda: regularisation weight. It must be a scalar > 0. If it is not provided it is estimated inside the function.
nsplits: number of splits of the dataset used to solve the regularised least square problem with an iterative approach (in order to save memory). In practice, instead of solving 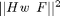, you can solve 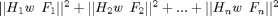, in which and . nsplits corresponds to n. A low value of nsplits makes ridgeRegression faster but it can result in memroy occupation problems. Default value, 1.
constraints: only if reducedComplexity = 0. array of structures defining optional constraints on the pwas function you want to obtain. Each element of the array defines different constraints. Tre structures have the following fields:

                - type: it can be either 'bounds' or 'equality'. If it
                        is 'bounds' constraints in the form
                        lbound <= f(x) <= ubound are imposed. lbound and
                        ubound can be provided through fields lbound and
                        ubound. If they are not provided they are
                        imposed as the minimum and maximum values of the
                        data Y and Yt contained in the dataset.
                        If type is equality, equality constraints in the
                        form f(x) = k can be imposed for x lying on a
                        hyper-plane parallel to the domain components.

                - lbound: lower bound for constraints of type 'bounds'

                - ubound: upper bound for constraints of type 'bounds'

                - variables: needed for equality constraints. It is an
                             array of strings indicating for which set of
                             points you want to impose the constraints. For
                             example if you want to impose a constraint
                             on f, for x1 = 3 and x3 = 2, variables must
                             be ['x1 = 3', 'x3 = 2'].

                - value: needed for equality constraints. It is the
                         value you want the function to assume in
                         correspondence of the points defined in field
                         variables. To impose the constraint f(x) = 0,
                         for x2 = 1 and x4 = 5 you gave to set
                         variables = ['x2 = 1', 'x4 = 5'] and value = 0.
* gamma: domain expansion parameter. If the domain D is not provided from
         outside the function, it is automatically extrapolated from data
         X. The tight domain (Dt) contains exactly data X. Such domain is
         grown of a factor gamma such as D = gamma Dt. Default value
         1.1.
* solver: string specifying the solver you want to use to solve the QP
          problem (this is necessary only for constrained ridge
          regression, otherwise the solution is analytical). Possible
          choices are 'quadprog' (default), 'cvx', 'cplex', 'yalmip'
          'clp'.
* verbose: if verbose is set to 1, messages are displayed indicating the
          status of the ridge regression process.

Acknowledgements

Contributors:

Tomaso Poggi (tpoggi@essbilbao.org)

IDENTIFY

Contents

Description

Syntax

Acknowledgements