PWAR

Piecewise Affine (hyper)Rectangular function object.

Description
Syntax
Properties
Public methods
Private methods
See also
Acknowledgements

Description

The pwar object describes a Piecewise Affine (hyper)Rectangular function, i.e. a PWA function defined on a domain partitioned into regular hyperrectangles. These are obtained by dividing each axis 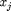$x_j$ of the state domain into 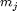$m_j$ segments. If these 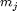$m_j$ segments on an axis have the same length, the partition is called uniform, otherwise it is called non-uniform.

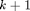A pwar function can also have a partition which is constructed from different levels of refinement, e.g. by subsequent refinement of some regions on each refinement level $k$ , yielding new regions on level $k+1$ . Such a function is called a multi-resolution function, distinct from the single-resolution case discussed above.

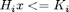The value of the function inside a rectangular region $i$ defined by constraints $H_{i} x <= K_{i}$ , is given by $u = F_{i}*x + G_{i}$ .

Syntax

fpwar = pwar()

Builds an empty pwar object.

fpwar = pwar(H, K, F, G, D)

Builds a pwar object from [1*nr] cells H, K, F and G containing the PWA function matrices, and a matrix D containing the domain.

Properties

nd - number of dimensions of the domain.
nf - number of dimensions of the codomain.
nr - number of regions of the partition of the domain.
H, K - cells defining the edges of the regions, in the form H{i}*x <= K{i}.
F, G - cells defining the coefficients of the affine functions on each polytope in the form y = F{i}*x + G{i}.
D - domain of definition of the function. see getDomain for details.
tree - orthogonal search tree associated to the domain partition, in case of a multi-resolution function.
details - a structure providing more in-depth information about the function and its origins, such as the grid type, approximation norm used, etc.
synthesisInfo - structure containing some information related to the circuit synthesis of the pwar function.

Public methods

disp - displays some information about the pwar object.
eval - evaluates the pwar function on a point or set of points.
findRegion - finds the polytope containing a given point.
getClosedLoop - constructs a pwag object of the pwar object in closed loop with a plant model.
getDomain - gets the domain over which the pwar function is defined.
getEdges - gets the edges of a region.
getFunctions - gets the coefficients of the affine function defined over a region.
getNumberOfDimensions - gets the number of dimensions of the domain of the pwar function.
getNumberOfEdges - gets the number of different edges of the domain partition.
getNumberOfFunctions - gets the number of different affine functions composing the pwar function.
getNumberOfRegions - gets the number of polytopes of the domain partition.
getPartition - gets the partition information.
getRegions - gets information about the requested polytope(s).
getSynthesisInfo - gets information about how the domain is scaled for the circuit synthesis.
getTree - gets the matrix containing the orthogonal search tree.
isSingleRes - queries whether the object has a single-resolution partition.
isUniform - queries whether the object has a uniform partition.
loadTestOutput - Loads the output of VHDL simulation and rescales values to original co-domain.
plot - plots the pwar function.
plotTree - plots the search tree associated to the domain partition.
sim - dummy to call linearSystem/sim.
simplot - dummy to call linearSystem/simplot.
synthesize - generates the VHDL files describing the digital circuit which implements the pwar function.

Private methods

computeFSM - Computes the finite state machine for circuit implementation.
writeFSM -Creates the VHDL code for the finite state machine of an mPWAR function implementation.
writeInputRegister - Writes the VHDL code for the input register file.
writeMemory - Generates n+1 memory blocks to store the coefficients of a PWAR function.
writePackage - Writes the VHDL code for the package file.
writePWLmodule - Writes the VHDL code for PWL module file.
writePWLmoduleTest - Writes the VHDL code for PWL module test file.
writeSynthesisLog - Writes some information about the FPGA synthesis to a log file.
writeTestInput - Generates a test file with inputs for the circuit.

Acknowledgements

Contributors:

Bart Genuit (b.a.g.genuit@tue.nl)